In a triangle ABC, AD is the median. F is the point on AC such that line BF bisect AD at E. Prove that AC = 3AF.
- Home
- Math
- All Questions
Answer:
Step by Step Explanation: - Following picture shows triangle ΔABC with median AD at E, and another line BF, which bisects AD. We have also drawn another line DG which is parallel to BF.
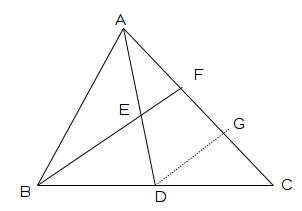
- From proportionality theorem we know that if a line is drawn parallel to one side of a triangle, it divides other two sides in the same ration.
- For triangle ΔBFC, DG is parallel to BF and using proportionality theorem we can find that,
= - Since we know that BD = DC, we can find that,
GC = FG ---------(1) - Similarly we can use proportionality theorem for triangle ΔADG,
= - But since AE = ED,
FG = AF ---------(2) - Therefore,
AC = AF + FG + GC
Using relation (1) and (2),
AC = AF + AF + AF,
AC = 3AF

 Philippines
Philippines
